GNU Radio 3.7.1 C++ API
Public Types | Static Public Member Functions
gr::analog::cpm Class Reference

Return the taps for an interpolating FIR filter (gr::filter::interp_fir_filter_fff). More...

#include <cpm.h>

List of all members.

Public Types

enum  cpm_type {
  LRC, LSRC, LREC, TFM,
  GAUSSIAN, GENERIC = 999
}

Static Public Member Functions

static std::vector< float > phase_response (cpm_type type, unsigned samples_per_sym, unsigned L, double beta=0.3)
 Return the taps for an interpolating FIR filter (gr::filter::interp_fir_filter_fff).

Detailed Description

Return the taps for an interpolating FIR filter (gr::filter::interp_fir_filter_fff).

Member Enumeration Documentation

enum gr::analog::cpm::cpm_type
Enumerator:
LRC 
LSRC 
LREC 
TFM 
GAUSSIAN 
GENERIC 

Member Function Documentation

static std::vector<float> gr::analog::cpm::phase_response ( cpm_type  type,
unsigned  samples_per_sym,
unsigned  L,
double  beta = 0.3 
) [static]

Return the taps for an interpolating FIR filter (gr::filter::interp_fir_filter_fff).

These taps represent the phase response 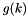$g(k)$ for use in a CPM modulator, see also gr_cpmmod_bc.

Parameters:
typeThe CPM type (Rectangular, Raised Cosine, Spectral Raised Cosine, Tamed FM or Gaussian).
samples_per_symSamples per symbol.
LThe length of the phase response in symbols.
betaFor Spectral Raised Cosine, this is the rolloff factor. For Gaussian phase responses, this the 3dB-time-bandwidth product. For all other cases, it is ignored.

Output: returns a vector of length K = samples_per_sym x L. This can be used directly in an interpolating FIR filter such as gr_interp_fir_filter_fff with interpolation factor samples_per_sym.

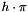All phase responses are normalised s.t. $ \sum_{k=0}^{K-1} g(k) = 1$; this will cause a maximum phase change of $ h \cdot \pi$ between two symbols, where h is the modulation index.

The following phase responses can be generated:

  • LREC: Rectangular phase response.
  • LRC: Raised cosine phase response, looks like 1 - cos(x).
  • LSRC: Spectral raised cosine. This requires a rolloff factor beta. The phase response is the Fourier transform of raised cosine function.
  • TFM: Tamed frequency modulation. This scheme minimizes phase change for rapidly varying input symbols.
  • GAUSSIAN: A Gaussian phase response. For a modulation index h = 1/2, this results in GMSK.

A short description of all these phase responses can be found in [1].

[1]: Anderson, Aulin and Sundberg; Digital Phase Modulation

The documentation for this class was generated from the following file: